
Rank nullity theorem YouTube
Rank Theorem. rank ( A )+ nullity ( A )= n . (dimofcolumnspan) + (dimofsolutionset) = (numberofvariables). The rank theorem theorem is really the culmination of this chapter, as it gives a strong relationship between the null space of a matrix (the solution set of Ax = 0 ) with the column space (the set of vectors b making Ax = b consistent.

rank nullity theorem matrix cucet 2017 linear algebra engineering mathematics csir net gate iit
The Rank Plus Nullity Theorem Let A be a matrix. Recall that the dimension of its column space (and row space) is called the rank of A. The dimension of its nullspace is called the nullity of A. The connection between these dimensions is illustrated in the following example. Example 1: Find the nullspace of the matrix
Rank Nullity Theorem YouTube
The rank of T, written rank T is dim im T. Example 4.16.1 . Returning to the differentiation example from the end of the last lecture, D : ℝ ⩽ n [ x ] → ℝ ⩽ n [ x ] has nullity 1 (since its kernel was one-dimensional, spanned by the constant polynomial 1) and rank n , since its image had a basis 1 , x ,. , x n − 1.

Rank and nullity of linear map, Rank and Nullity Theorem YouTube
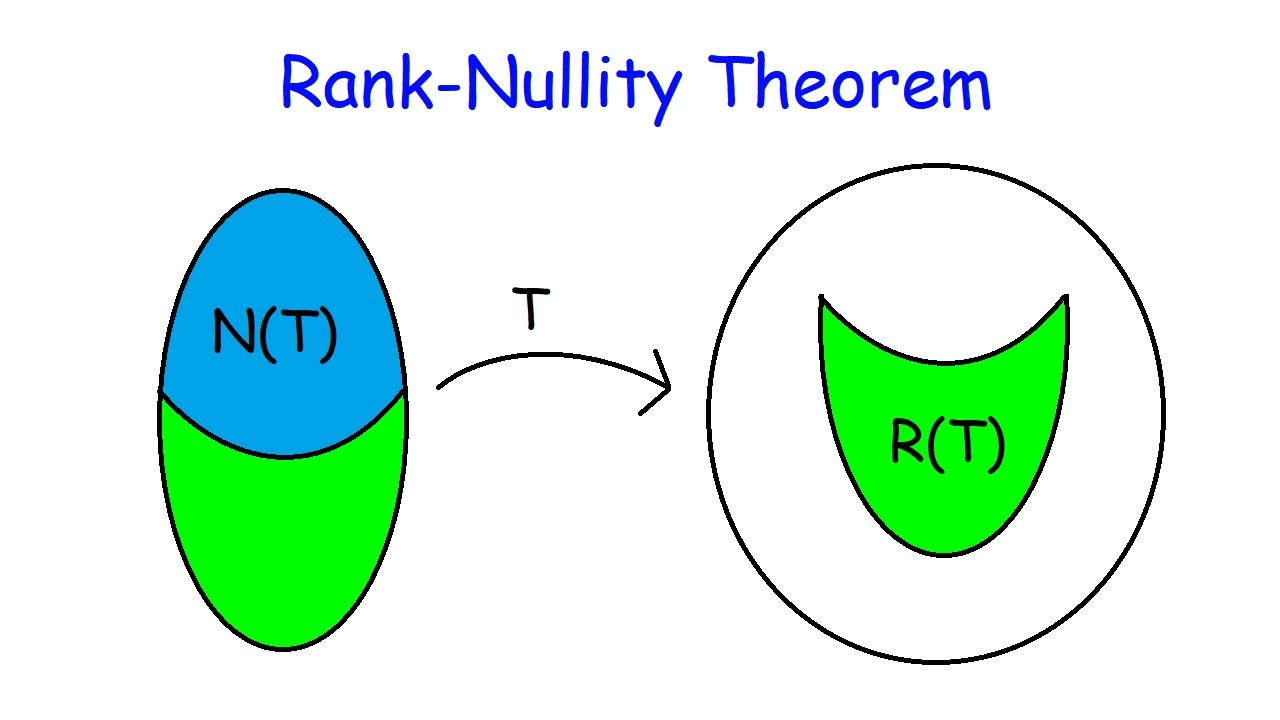
The rank-nullity theorem is a theorem in linear algebra, which asserts: the number of columns of a matrix M is the sum of the rank of M and the nullity of M; and the dimension of the domain of a linear transformation f is the sum of the rank of f (the dimension of the image of f) and the nullity of f (the dimension of the kernel of f ).

Rank nullity theorem
Rank-Nullity Theorem Let and be vector spaces over a field , and let be a linear transformation . Assuming the dimension of is finite, then where is the dimension of , is the kernel, and is the image . Note that is called the nullity of and is called the rank of . See also Kernel, Null Space, Nullity, Rank This entry contributed by Rahmi Jackson

Ranknullity theorem Lecture notes 22 Applied Mathematics StuDocu
The Rank-Nullity Theorem helps here! Linear Algebra Dimension, Rank, Nullity Chapter 4, Sections 5 & 6 9 / 11. Example Suppose A is a 20 17 matrix. What can we say about A~x = ~b? Recall that NS(A) is a subspace of R17 and CS(A) is a subspace of R20.

MATH0005 L59 the ranknullity theorem YouTube
Example 2.9. 1: Rank and nullity. Here is a concrete example of the rank theorem and the interplay between the degrees of freedom we have in choosing x and b in a matrix equation A x = b. Consider the matrices. A = ( 1 0 0 0 1 0 0 0 0) and B = ( 0 0 0 0 0 0 0 0 1). If we multiply a vector ( x, y, z) in R 3 by A and B we obtain the vectors A x.

Rank Nullity Theorem Example 2 Linear Algebra Griti YouTube
The rank-nullity theorem states that the dimension of the domain of a linear function is equal to the sum of the dimensions of its range (i.e., the set of values in the codomain that the function actually takes) and kernel (i.e., the set of values in the domain that are mapped to the zero vector in the codomain). Linear function

Rank Theorem (RankNullity Thm), 4 Fundamental Subspaces, Invertible Matrix Theorem, Change of
The rank-nullity theorem states that the rank and the nullity (the dimension of the kernel) sum to the number of columns in a given matrix. If there is a matrix \ (M\) with \ (x\) rows and \ (y\) columns over a field, then \ [\text {rank} (M) + \text {nullity} (M) = y.\]

Rank nullity theorem for matrices YouTube
University of Oxford mathematician Dr Tom Crawford introduces the concepts of rank and nullity for a linear transformation, before going through a full step-.

Linear Algebra Lecture 39 Rank Nullity Theorem for Linear Transformations YouTube
The Rank of a Matrix is the Dimension of the Image Rank-Nullity Theorem Since the total number of variables is the sum of the number of leading ones and the number of free variables we conclude: Theorem 7. Let M be an n m matrix, so M gives a linear map M : Rm!Rn: Then m = dim(im(M)) + dim(ker(M)): This is called the rank-nullity theorem.

Math 2.9.8. Rank nullity theorem YouTube
The Rank-Nullity Theorem Definition 1. The dimension of a non-zero subspace, H, denoted dim H, is the number of vectors in any basis for H. The dimension of the zero subspace f0g is zero. Definition 2. The rank of a matrix, A 2 Rm n, denoted rank A, is the dimension of the column space of A, rank A = dim (Col(A)) :

Linear Algebra Part 35 RankNullity Theorem YouTube
Rank Theorem. rank ( A )+ nullity ( A )= n . (dimofcolumnspan) + (dimofsolutionset) = (numberofvariables). The rank theorem theorem is really the culmination of this chapter, as it gives a strong relationship between the null space of a matrix (the solution set of Ax = 0 ) with the column space (the set of vectors b making Ax = b consistent.

Sec 4.8 Example 1 Kernel, range, and ranknullity for a linear transformation YouTube
Very loosely, I think of the rank-nullity theorem as saying: What you end up with is what you start with minus what you lose. "What you end up with" being the rank, "what you start with" being the dimension of the domain space, and "what you lose" being the nullity. - Daniel Schepler Apr 19, 2019 at 19:37 Add a comment

Rank Nullity Theorem Proof and Explanation of Meaning of Range Space , Column Space and Null
Rank-nullity theorem The nullity (dimension of the nullspace) and the rank (dimension of the range) of a matrix add up to the column dimension of , . Proof: Let be the dimension of the nullspace ( ). Let be a matrix such that its columns form an orthonormal basis of . In particular, we have .

4.16 the ranknullity theorem YouTube
4.9 The Rank-Nullity Theorem In Section 4.3, we defined the null space of a real m n matrix × A to be the set of all real solutions to the associated homogeneous linear system Ax 0. Thus, = nullspace(A) {x n = ∈ R Ax : 0 = }. The dimension of nullspace(A) is referred to as the nullity of A and is denoted nullity(A).