
Area and Volume of Similar Shapes (B) Worksheet Fun and Engaging PDF Worksheets
This video explains how areas are connected for similar shapes. It also covers surface areas.
Area of Similar Figures IGCSE at Mathematics Realm
GCSE Maths revision tutorial video.For the full list of videos and more revision resources visit www.mathsgenie.co.uk.

Area and Volume of Similar Shapes (A) Worksheet Cazoom Maths Worksheets
The Relation between the Area of Similar Figures. When two figures are similar, the square of the ratio of their corresponding side lengths equals the ratio of their area. When the ratio of two corresponding sides (or other lengths) is expressed as \ (\frac {a} {b}\), in similar figures, the ratio of the areas is expressed as \ (\frac {a^2} {b^2}\)
Area of Similar Figures
Start Lesson Back In this lesson, we will identify similar shapes and subsequently work out areas of similar shapes using our knowledge of scale factors.

Similar Shapes Area Volume Textbook Exercise Corbettmaths
A video revising the techniques and strategies for looking at similar shapes with area and volume. (Higher Only).This video is part of the Ratio & Proportion.

Similar Shape Volumes Video Corbettmaths
How to find lengths/area using lengths/area.

Similar Shapes (Area and Volume) Teaching Resources
Unit 1 Lines Unit 2 Angles Unit 3 Shapes Unit 4 Triangles Unit 5 Quadrilaterals Unit 6 Coordinate plane Unit 7 Area and perimeter Unit 8 Volume and surface area Unit 9 Pythagorean theorem Unit 10 Transformations Unit 11 Congruence Unit 12 Similarity Unit 13 Trigonometry Unit 14 Circles Unit 15 Analytic geometry Unit 16 Geometric constructions

Volume and Surface Area of similar shapes example. YouTube
Solution: Linear scale factor = 4 Area scale factor = 42 ( = 16 ) New surface area: 3.5 × 16 = 56 m2 Volume scale factor: If we take a cuboid of length 3 cm and breadth 2 cm 4 cm and height 4 cm then the 3 cm 2 cm Volume = 3 × 2 × 4 = 24 cm3.

Similar Shapes (Area and Volume) GCSE maths grade 6
Videos, worksheets, 5-a-day and much more. Menu Skip to content. Welcome; Videos and Worksheets; Primary; 5-a-day. 5-a-day GCSE 9-1

PPT 10.4 Perimeters and Areas of Similar Figures PowerPoint Presentation ID6031832
Lesson 1: Similar shapes. Explains the definition of similar shapes and how to prove they are similar by finding all angles and sides are the same. Examples of how to find an use scale factor to prove this. Independent questions for students to work on with an exam style question for extension work.

Area and Perimeter of Similar Figures YouTube
Edexcel Transformations - Edexcel Scale factors of similar shapes - Higher Transformations change the size or position of shapes. Congruent shapes are identical, but may be reflected,.

G19a Lengths, areas and volumes in similar shapes
The Corbettmaths video tutorial on Similar Shapes - Areas. Videos, worksheets, 5-a-day and much more

Similar Shapes Area & Volume Videos Corbettmaths
Volume To Surface Area Scaling137/D. Calculate the surface area of a similar 3d shape where it is possible to deduce the volume scale factor directly. Questions Lesson. Maths Kitchen provides easy to use, high quality resources and personalised revision guidance for GCSE Maths.

Areas of similar shapes (3 of 5) YouTube
Area of Similar Shapes How to measure Volume of Similar Shapes How to measure Solved Examples : Key Facts and Summary Recommended Worksheets Introduction Similar shapes are the shapes that have corresponding sides in proportion to every alternative and corresponding angles adequate to each other.
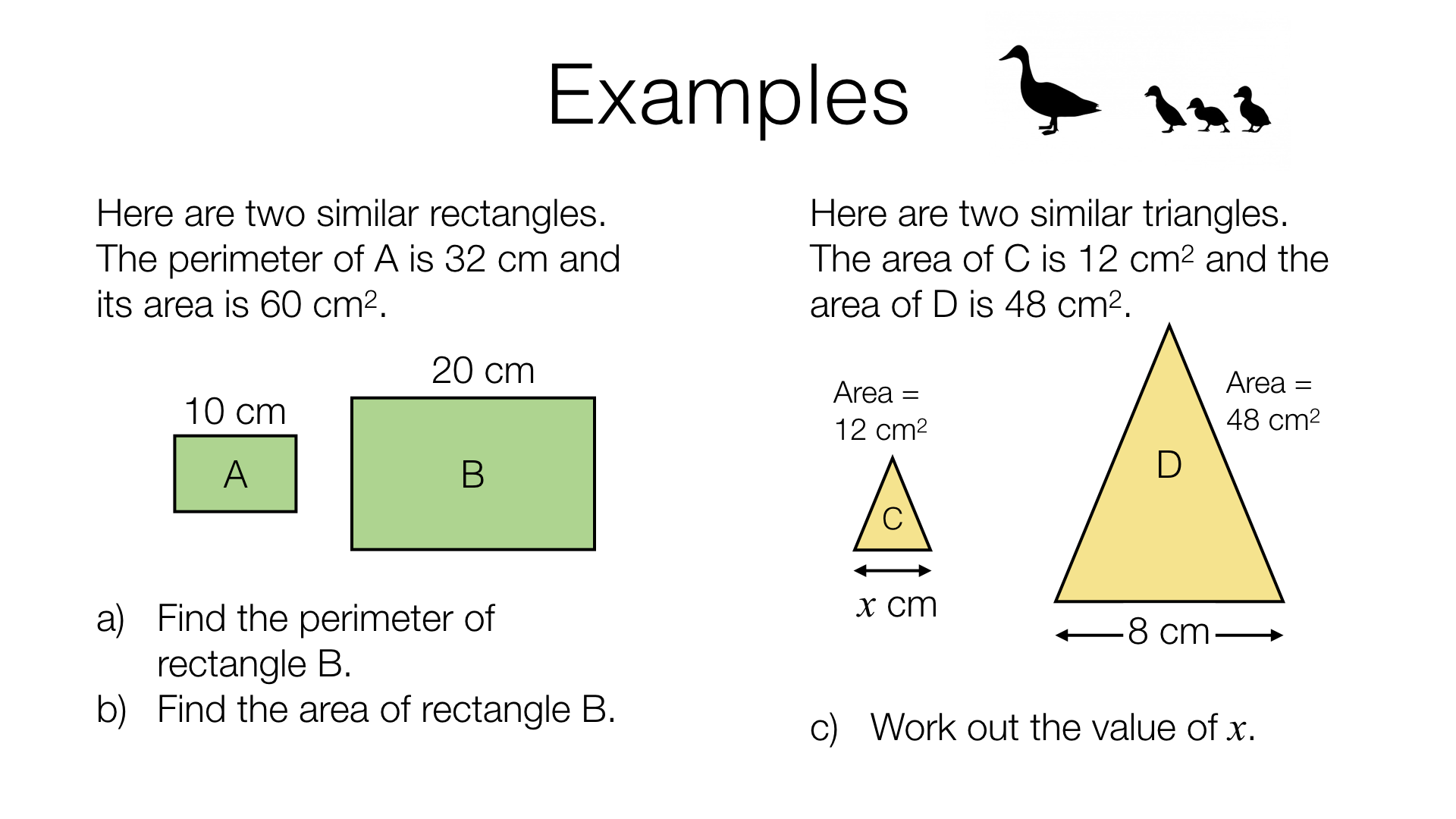
G19a Lengths, areas and volumes in similar shapes
The ratio of the area of two similar triangles is equal to the square of the ratio of any pair of the corresponding sides of the similar triangles. If two triangles are similar it means that: All corresponding angle pairs are equal and all corresponding sides are proportional.

G19a Lengths, areas and volumes in similar shapes
Two solids are similar if they are the same type of solid and their corresponding radii, heights, base lengths, widths, etc. are proportional. Surface Areas of Similar Solids. In two dimensions, when two shapes are similar, the ratio of their areas is the square of the scale factor. A comparable relationship holds in three dimensions as well.